I/Định nghĩa :
Cây là cấu trúc dữ liệu dùng để lưu trữ một tập các dữ liệu có cùng kiểu và các dữ liệu này được lưu trữ không liên tiếp trong bộ nhớ . Mỗi nút (phần tử) trên cây sẽ giữ địa chỉ của nút con bên trái và địa chỉ của nút con bên phải , khi đó chỉ cần biết địa chỉ nút gốc (nút không là con của bất kỳ nút nào ) là có thể truy xuất đến tất cả các nút .
Danh sách liên kết đơn là trường hợp đặc biệt của cây nhị phân mà tất cả các nút chỉ con trái hoặc tất cả các nút chỉ con phải .
II/Các loại cây nhị phân :
II.1/Cây nhị phân tìm kiếm (Binary Search Tree-Hình 1)

Với mọi nút p , dữ liệu của các nút trên cây con trái của p <= dữ liệu nút p <= dữ liệu của các nút trên cây con phải của p .
II.2/Cây nhị phân đúng (Strictly Binary Tree-Hình 2)
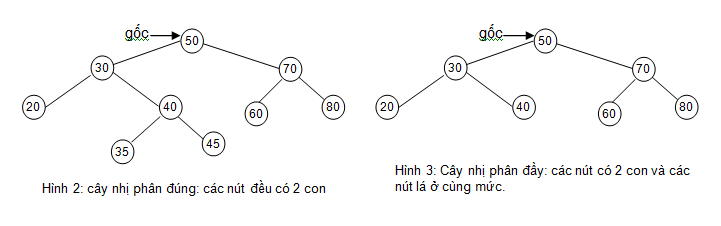
Tất cả các nút đều có 2 con , ngoại trừ nút lá .
II.3/Cây nhị phân đầy (Complete Binary Tree-Hình 3)

Là cây nhị phân đúng và tất cả các nút lá ở cùng mức .
Nếu cây có chiều cao h thì số nút của cây là N = 2^(h+1) - 1 ==> h = log2(N+1) -1 . Vậy chiều cao của cây nhỏ hơn rất nhiều so với tổng số nút ==> Tìm kiếm nhanh .
Cây nhị phân đầy sẽ có đầy đủ các nút ở mỗi mức .
II.4/Cây nhị phân gần đầy(Almost Complete Binary Tree)
Tất cả các mức <=h-1 (h là chiều cao của cây) có đầy đủ các nút , còn ở mức h , các nút đầy từ trái sang phải .
III/Ưu khuyết điểm cây nhị phân tìm kiếm :
III.1/Ưu điểm :
Có được ưu điểm của danh sách liên kết như là : Thao tác hủy hoặc chèn rất nhanh , có thể cấp phát thêm nút hoặc thu hồi bộ nhớ đã cấp phát cho nút và kích thước cây không bị giới hạn bởi 64 KB .
Có thêm ưu điểm khác là tìm kiếm nhanh (trong khi danh sách liên kết tìm kiếm chậm).
III.2/Khuyết điểm :
Tốn thêm bộ nhớ để lưu trữ địa chỉ nút con trái , con phải .
IV/Các hàm xử lý cây nhị phân tìm kiếm :
IV.1/Khai báo cấu trúc một nút :
IV.2/Hàm khởi tạo cây :
Khởi tạo cây là làm cho cây rỗng bằng cách gán root = NULL
IV.3/Hàm kiểm tra cây rỗng :
Nếu root = NULL thì cây rỗng , và hàm trả về giá trị 1 , ngược lại trả về 0
IV.4/Hàm tạo một nút :
Cấp phát bộ nhớ cho một nút , cất dữ liệu vào nút , gán left , right == NULL , trả về địa chỉ nút.
IV.5/Hàm chèn một nút :
Chèn nút chứa dữ liệu x vào cây có gốc là root và trả về địa chỉ nút mới chèn.
IV.6/ Hàm tìm nút :
Tìm nút chứa x trên cây có gốc là root , nếu tìm thấy trả về địa chỉ nút chứa x , ngược lại trả về NULL.
IV.7/ Hàm hủy nút :
Gọi p là nút cần hủy , có ba trường hợp :
a/ p không có con :
delete p;
b/ p có một con :
Gọi f là cha p , q là con p .
Cho q là con của f .
delete p ;
c/ p có 2 con : đưa về trường hợp hủy nút có không con hoặc một con bằng cách :
+) Tìm nút thế mạng q
q là nút cực trái của cây con phải của p hoặc q là nút cực phải của của cây con trái của p .
q sẽ có không con hoặc một con .
+) Chép dữ liệu q vào p .
+) Hủy q .
IV.8/ Hàm tạo cây :
Nhập vào n số nguyên , lưu vào cây nhị phân tìm kiếm .
IV.9/ Hàm duyệt cây :
Có 6 phương pháp duyệt cây : NLR , LNR ; LRN ; NRL ; RNL ; RLN . Ba phương pháp sau tương tự với 3 phương pháp đầu nên ta chỉ xét 3 phương pháp đầu .
a/ Node - Left - Right :
Duyệt nút gốc - Duyệt cây con trái - Duyệt cây con phải .
b/ Left - Node - Right :
Duyệt cây con trái - Duyệt nút gốc - Duyệt cây con phải .
Phương pháp duyệt này sẽ cho dãy tăng .(RNL sẽ cho dãy giảm)
c/ Left - Right - Node :
Duyệt cây con trái - Duyệt cây con phải - Duyệt nút gốc .
IV.10/ Hàm hủy cây :
Thu hồi bộ nhớ đã cấp phát cho tất cả các nút trên cây , làm cho cây rỗng .
Cây là cấu trúc dữ liệu dùng để lưu trữ một tập các dữ liệu có cùng kiểu và các dữ liệu này được lưu trữ không liên tiếp trong bộ nhớ . Mỗi nút (phần tử) trên cây sẽ giữ địa chỉ của nút con bên trái và địa chỉ của nút con bên phải , khi đó chỉ cần biết địa chỉ nút gốc (nút không là con của bất kỳ nút nào ) là có thể truy xuất đến tất cả các nút .
Danh sách liên kết đơn là trường hợp đặc biệt của cây nhị phân mà tất cả các nút chỉ con trái hoặc tất cả các nút chỉ con phải .
II/Các loại cây nhị phân :
II.1/Cây nhị phân tìm kiếm (Binary Search Tree-Hình 1)

Với mọi nút p , dữ liệu của các nút trên cây con trái của p <= dữ liệu nút p <= dữ liệu của các nút trên cây con phải của p .
II.2/Cây nhị phân đúng (Strictly Binary Tree-Hình 2)

Tất cả các nút đều có 2 con , ngoại trừ nút lá .
II.3/Cây nhị phân đầy (Complete Binary Tree-Hình 3)

Là cây nhị phân đúng và tất cả các nút lá ở cùng mức .
Nếu cây có chiều cao h thì số nút của cây là N = 2^(h+1) - 1 ==> h = log2(N+1) -1 . Vậy chiều cao của cây nhỏ hơn rất nhiều so với tổng số nút ==> Tìm kiếm nhanh .
Cây nhị phân đầy sẽ có đầy đủ các nút ở mỗi mức .
II.4/Cây nhị phân gần đầy(Almost Complete Binary Tree)
Tất cả các mức <=h-1 (h là chiều cao của cây) có đầy đủ các nút , còn ở mức h , các nút đầy từ trái sang phải .
III/Ưu khuyết điểm cây nhị phân tìm kiếm :
III.1/Ưu điểm :
Có được ưu điểm của danh sách liên kết như là : Thao tác hủy hoặc chèn rất nhanh , có thể cấp phát thêm nút hoặc thu hồi bộ nhớ đã cấp phát cho nút và kích thước cây không bị giới hạn bởi 64 KB .
Có thêm ưu điểm khác là tìm kiếm nhanh (trong khi danh sách liên kết tìm kiếm chậm).
III.2/Khuyết điểm :
Tốn thêm bộ nhớ để lưu trữ địa chỉ nút con trái , con phải .
IV/Các hàm xử lý cây nhị phân tìm kiếm :
IV.1/Khai báo cấu trúc một nút :
Mã:
struct node
{
int data;//Noi dung cua nut
node *letf , *right;//Dia chi nut trai , nut phai
};
typedef node *nodeptr;Khởi tạo cây là làm cho cây rỗng bằng cách gán root = NULL
Mã:
void init_tree(nodeptr &root)
{
root = NUll;
}Nếu root = NULL thì cây rỗng , và hàm trả về giá trị 1 , ngược lại trả về 0
Mã:
int empty_tree(nodeptr root)
{
if(root == NULL) return 1;
else return 0;
}Cấp phát bộ nhớ cho một nút , cất dữ liệu vào nút , gán left , right == NULL , trả về địa chỉ nút.
Mã:
nodeptr make_node(int x)
{
noteptr p = new node;
p->data = x;
p->left = p->right = NULL;
return p;
}Chèn nút chứa dữ liệu x vào cây có gốc là root và trả về địa chỉ nút mới chèn.
Mã:
nodeptr insert_node(nodeptr &root , int x)
{
nodeptr p =make_node(x) ;
nodeptr q,f;
if(root == NULL)
{
root = p;
}
else
{
root = q;
f=NULL;
while(q!=NULL)
{
f = q;
if(x < q ->data)
{
q = q->left;
}
else
{
q = q->right;
}
}
if(x < f->data)
{
f->left = p;
}
else
{
f->right = p;
}
}
return p;
}Tìm nút chứa x trên cây có gốc là root , nếu tìm thấy trả về địa chỉ nút chứa x , ngược lại trả về NULL.
Mã:
nodeptr search_node(nodeptr root , int x)
{
nodeptr p = root;
while(p!=NULL)
{
if(p->data == x) return p;
else if(x < p->data) p = p->left;
else p = p->right;
}
return NULL;
}Gọi p là nút cần hủy , có ba trường hợp :
a/ p không có con :
delete p;
b/ p có một con :
Gọi f là cha p , q là con p .
Cho q là con của f .
delete p ;
c/ p có 2 con : đưa về trường hợp hủy nút có không con hoặc một con bằng cách :
+) Tìm nút thế mạng q
q là nút cực trái của cây con phải của p hoặc q là nút cực phải của của cây con trái của p .
q sẽ có không con hoặc một con .
+) Chép dữ liệu q vào p .
+) Hủy q .
Mã:
int del_node(nodeptr &root , int x)
{
nodeptr p , q , f;
p = root;
f = NULL;
while(p!=NULL)
{
if(p->data == x) break;
else
{
f = p;
if(x<p->data) p = p->left;
else p = p->right;
}
}
if(p==NULL) return 0;
else
{
if(p->left !=NULL && p->right!=NULL)
{
q = p->right;
f = p;
while(q->left!=NULL)
{
f = q;
q = q->left;
}
p->data = q->data;
p = q;
}
if(p->left!=NULL) q = p->left;
else q = p->right;
if(p==root) root = q;
else
{
if(p=f->left) f->left = q;
else f->right = q;
}
delete p;
return 1;
}
}Nhập vào n số nguyên , lưu vào cây nhị phân tìm kiếm .
Mã:
void input_tree(nodeptr &root)
{
int n,x;
root = NULL;
printf("\nSo phan tu : ");
scanf("%d" , &n);
for(int i=1; i<=n; i++)
{
printf("Phan tu thu %d : ",i);
scanf("%d" , &x);
insert_node(root , x);
}
}Có 6 phương pháp duyệt cây : NLR , LNR ; LRN ; NRL ; RNL ; RLN . Ba phương pháp sau tương tự với 3 phương pháp đầu nên ta chỉ xét 3 phương pháp đầu .
a/ Node - Left - Right :
Duyệt nút gốc - Duyệt cây con trái - Duyệt cây con phải .
Mã:
void NLR(nodeptr root)
{
if(root!=NULL)
{
printf("%d" , root->data);
NLR(root->left);
NLR(root->right);
}
}Duyệt cây con trái - Duyệt nút gốc - Duyệt cây con phải .
Phương pháp duyệt này sẽ cho dãy tăng .(RNL sẽ cho dãy giảm)
Mã:
void LRN(nodeptr root)
{
if(root!=NULL)
{
LNR(root->left);
printf("%d" , root->data);
LNR(root->right);
}
}Duyệt cây con trái - Duyệt cây con phải - Duyệt nút gốc .
Mã:
void LRN(nodeptr root)
{
if(root!=NULL)
{
LRN(root->left);
LRN(root->right);
printf("%d" , root->data);
}
}Thu hồi bộ nhớ đã cấp phát cho tất cả các nút trên cây , làm cho cây rỗng .
Mã:
void del_tree(nodeptr &root)
{
if(root!=NULL)
{
del_tree(root->left);
del_tree(root->right);
delete root;
root = NULL;
}
}